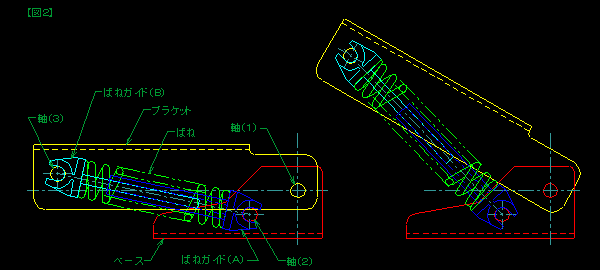
 【図2】はヒンジ部分を記したものです。 【図2】はヒンジ部分を記したものです。
左側はADFを閉めた状態、右側は任意の角度に開い
た状態です。
隠線処理はしていません。(業種によって判断基準
が違いますが、私はこの描き方で育ちました)
外見では1つの軸だけで回転する装置ですが、実際
には3つの軸があります。
軸(1)がヒンジの回転中心。
軸(2)、(3)はばねの荷重作用点です。
軸(2)と軸(3)との「距離」はヒンジの回転角度に
よって変化します。
また、軸(1)と軸(2)を結ぶ直線と、軸(2)と軸(3)を結ぶ直線によってできる「角度」も、ヒンジの回転角度によって変化します。
この「距離」と「角度」の変化でカウンターバランスヒンジのトルク特性を生み出します。 |
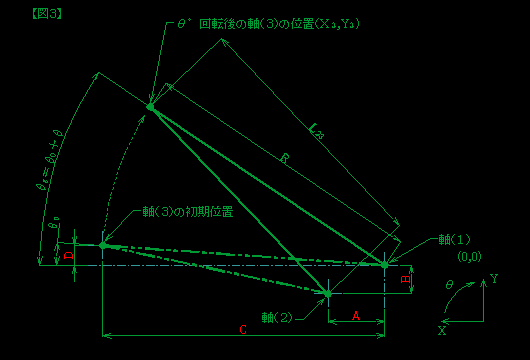 【図3】は【図2】を模式化したものです。 【図3】は【図2】を模式化したものです。
この図をもとにして計算式を作ります。
図中に赤色で記した4つの寸法は変数で、要求されるトルク特性に
応じた値を設定します。 |
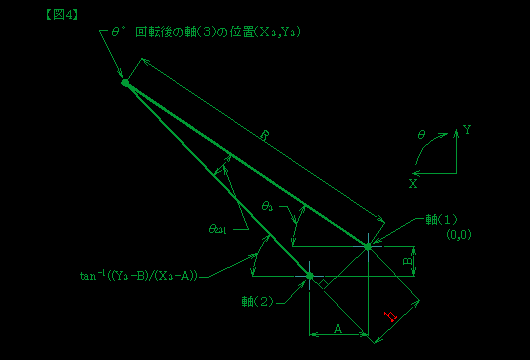 n【図4】は【図3】と同じものですが、最終的に求めようとする値「h」 n【図4】は【図3】と同じものですが、最終的に求めようとする値「h」
(図中の赤色)の計算式を作るための補助的な図です。
求めるトルクは 「h」×「ばね荷重」 となります。
途中の計算式を省略して結論だけを書くと、次の式になります。
h = R・sin(tan-1((Y3-B)/(X3-A))-tan-1(D/C)+θ))
R , Y3 , X3 には下記の式を代入します。
R = √(C2+D2)
Y3 = R・sin(tan-1(D/C)+θ)
X3 = R・cos(tan-1(D/C)+θ) |
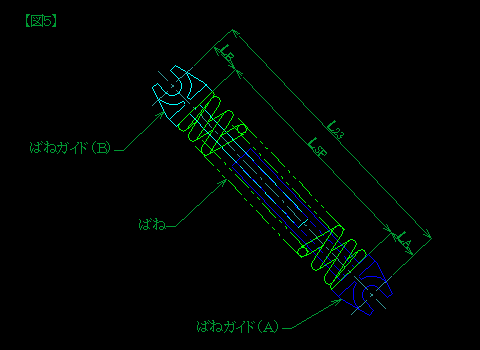 次に、ばねの取付け高さを求めます。 次に、ばねの取付け高さを求めます。
軸(2)と軸(3)の距離 「L23」 は次の式で求められます。
L23 = √((X3-A)2+(Y3-B)2)
X3 , Y3 は前述の値です。
「LSP」 は 「L23」 から、ばねガイドの寸法を差し引いた値です。
LSP = √((X3-A)2+(Y3-B)2)-LA-LB
そこで、ばね荷重 P は
P = (L-LSP)・k = (L-√((X3-A)2+(Y3-B)2)-LA-LB)・k
L : ばねの自由長 k : ばね定数 |
前述の通り、求めるトルク T は 「h」×「ばね荷重」ですから
T = (R・sin(tan-1((Y3-B)/(X3-A))-tan-1(D/C)+θ)))・(L-√((X3-A)2+(Y3-B)2)-LA-LB)・k
R = √(C2+D2)
Y3 = R・sin(tan-1(D/C)+θ)
X3 = R・cos(tan-1(D/C)+θ)
として求めることが出来ます。
では、具体的な数値を与えて計算します。
計算はこちら(右クリックから対象をファイルに保存を選択してダウンロードできます)の計算式を使います。
利用方法はこちらへ。
尚、この計算式は、自己の責においてご利用下さい。
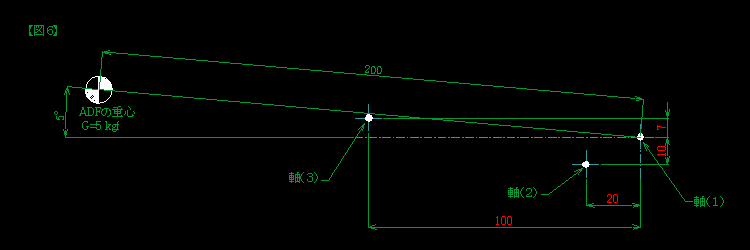
【図6】に示した数値の内、ADFの重心の位置は条件となる数値で、軸(1)を原点とした軸(2)、軸(3)の位置は数回の試行錯誤を繰り返した結果の数値です。
計算式によって得られたトルク特性が、下のグラフです。
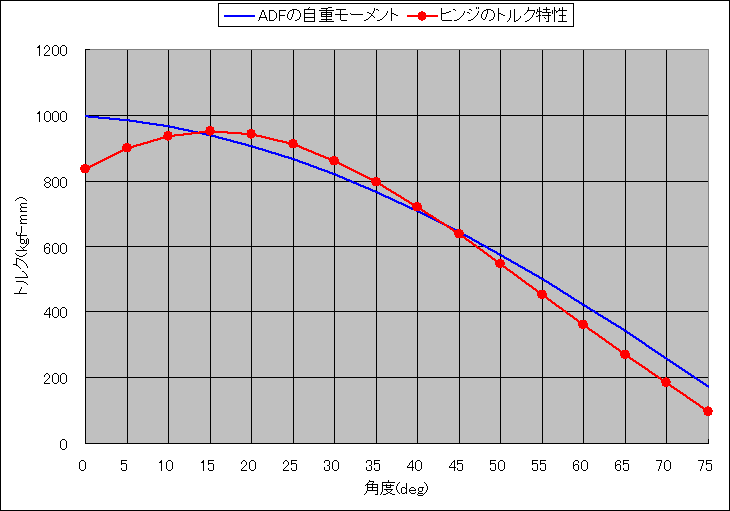
この曲線では、開角度13°付近および43°付近でADFの自重モーメントとヒンジのトルクが一致していることが解ります。
数値の一致した部分ではバランスがとれて、その開角度で静止できます。
実際にはばね荷重による摩擦力が発生しますので、ヒンジのトルクは幾分の幅を持ちます。
経験的には、約8°付近から55°付近までが静止の領域になりそうです。
0°では自重モーメントとヒンジのトルクの差が広がっていますが、ADFが原稿をコンタクトガラスに圧着するための力として、このようなトルク特性にします。
計算式の利用方法
ダウンロードしたファイルを開くと下記のような画面が現れます。
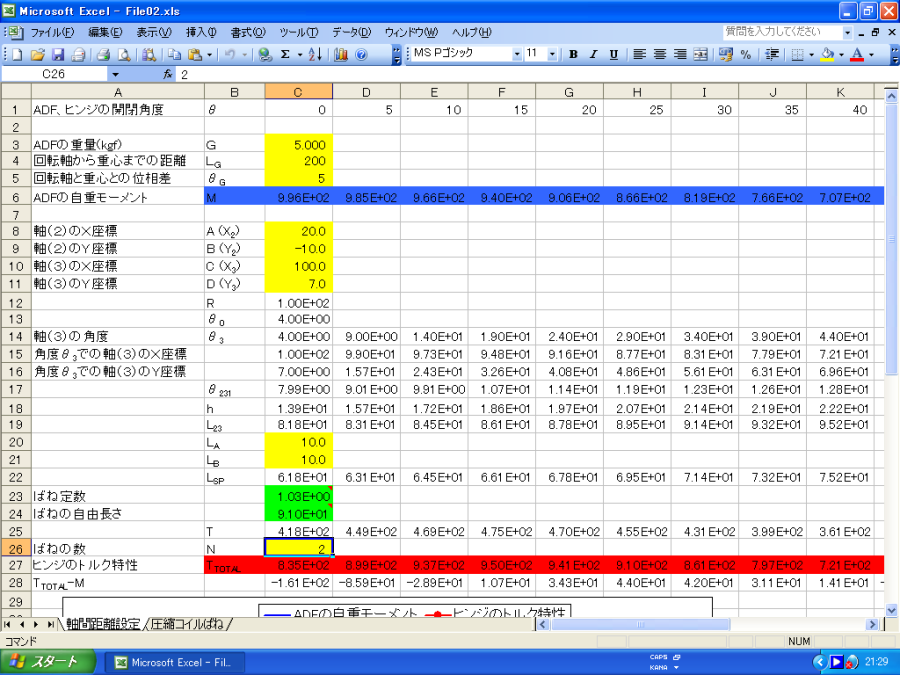
ファイルを開いた直後は「軸間距離設定」というシートが開きます。
このシートの黄色で網掛された部分が変更可能な変数です。他のセルは保護されています。
「ばねの数」の部分を「2」としていますが、実際にはヒンジを2個使用しました。
緑色で網掛されたセルはばねの設計に関するもので、「圧縮コイルばね」のシートで設計します。

こちらのシートも黄色の網掛部分が設定すべき変数です。
「材質」「線径」「両端研磨」についてはドロップダウンリストの中から選択して下さい。
B18、B19のセルに現される数値はばねの寿命に関するものです。詳しくはこちらへ。
「軸間距離の設定」と「圧縮コイルばね」の設定を繰り返しながら設計を進めます。 |